傅立叶变换榜上有名
傅立叶变换百科
1807年傅里叶提出概念
1807年傅里叶提出概念
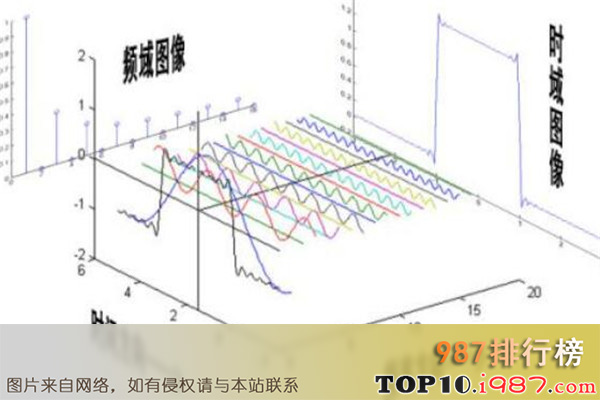
傅里叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。
在不同的研究领域,傅里叶变换具有多种不同的变体形式,如连续傅里叶变换和离散傅里叶变换。最初傅里叶分析是作为热过程的解析分析的工具被提出的。
傅立叶变换在《世界最美的十大数学公式》(2019年七月榜单数据)中上榜排名第四,前后上榜的分别为“圆的周长公式”、“麦克斯韦方程组”、“薛定谔方程”、“勾股定理”。
上榜理由:
傅立叶变换虽然很美,但相对来说是很难被理解通透的一个数学公式,它的出现对当代电子计算机的发展可以说是起到了重要在的推动作用。
傅立叶变换在《世界最伟大的十大公式》(2019年七月榜单数据)中上榜排名第一,前后上榜的分别为“薛定谔方程”、“牛顿第二定律”、“1+1=2”、“毕达哥拉斯定理”。
上榜理由:
在世界最伟大的十大公式中傅立叶变换对于不喜欢数学的朋友们来说可能就很难懂了,简单讲它的出现对数字频率领域有很大的推动作用,而且支持任何不规则信号的变换。
傅立叶变换在《世界最美的十大公式》(2019年七月榜单数据)中上榜排名第四,前后上榜的分别为“薛定谔方程”、“毕达哥拉斯定理”、“麦克斯韦方程组”、“牛顿第二定律”。
上榜理由:
傅立叶变换是高数中非常美的一个公式,也是让许多朋友吃不消的公式,它的出现是如今的互联网和数字信号等领域有着很重要的理论基础。
声明:i987十大排行榜所提供的“傅立叶变换”相关榜单数据是跟据联网大数据(如财报、网友投票、网友评分、第三方网站等)整理所得,数据不适用于对数据精确度及严谨性有要求的如科研、商业报告等使用。排名数据仅作参考,并不代表本身的好坏;数据来自互联网,本站对排名先后及是否入榜的数据不作人工干预,如有侵权请与我们联系。